Machine Learning
TensorFlow, Mini-Batch Gradiente Descendente Con Momento
A través de este post explicaremos la modificación del algoritmo del gradiente descendente aplicando el momento y sus consecuencias. Ademas, aunque ya existe la implementación en TensorFlow, construiremos el algoritmo modificando los gradientes antes de aplicarlos.
Gradiente Descendente con Momento (Gradient Descent With Momentum)
Descripción
El momento consiste en tener en cuenta la trayectoria anterior en un porcentaje definido por la tasa del momento que varia entre 0 y 1 donde los valores usuales son 0.5,0.9 y 0.95 si hubiéramos que elegirlo por medio de validación cruzada.
[latex]{\large variable = variable-\boldsymbol{lr}*acumulador}[/latex]
m es el coeficiente de Momento y lr es la tasa de aprendijaze
Como vemos en la formula, la trayectoria definida por el acumulador no puede variar bruscamente por el cambio de gradiente, dicho de otro modo: actúa como un filtro paso bajo. Eso se traduce en dos ventajas princiales:
- Evita sobreajuste: Si por la trayectoria alcanzamos un mínimo local, el gradiente descendente tiene muchas mas posibilidades de pararse que aplicando el momento puesto que gracias al acumulador podría pasar de largo, bordeando el mínimo local.
- Aumento de la Velocidad: El gradiente descendente va alcanzando el mínimo local siguiendo la trayectoria de mínima energía aunque sea el camino mas largo mientras que aplicando el momento, como se puede apreciar en la ilustración de abajo, no puede variar bruscamente el trayectoria y puede filtrar pequeñas fluctuaciones. Este punto será clave para entender el análisis de las gráficas de ECM vs iteraciones.
- Aumenta la convergencia: En los algoritmos como Mini-Batch o SGD, es muy recomendable utilizar el momento para suavizar la trayectoria y no sea tan zip-zap y en una de ellas no fuéramos de la trayectoria correcta
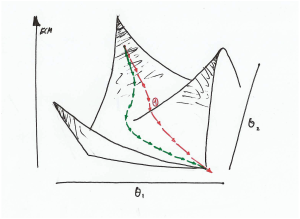
Trayectoria del algoritmo con Momento
Aplicando el Momento se aprecia que el algoritmo tiene la inercia suficiente para no tener en cuenta pequeñas alteriones (curva roja).
Implementación
Aunque el algoritmo ya está implementado en TensorFlow instanciando la Clase MomentumOptimizer, vamos a implementarlo instanciando la Clase GradientDescentOptimizer y en vez de aplicar el momento directamente a la variable por medio del metodo minimize() descompondremos en 3 pasos el calculo del algoritmo (de esta manera se podrá comprobar que podremos describir cualquier modelo a partir de una lista de gradientes ya calculados):
- Calculamos los gradientes para las variables definidas por medio
compute_gradients(), Nos devuelve una lista de tuplas (gradiente, variable) - Luego modificaremos los gradientes tal como se indica en la formula del Momento
- Y por ultimo aplicamos los gradientes modificados llamando al método
apply_gradients()
Algoritmo GradientDescent With Momentum
Hay que tener en cuenta que el metodo apply_gradients ya aplica la tasa de aprendizaje al gradiente por lo que no debemos caer en el error de aplicarlo dos veces
tf.control_dependencies: Si se nos olvida aparentemente el algoritmo funciona correctamente pero realmente estaremos aplicando los gradientes sin tener en cuenta el Momento.Demostración
Se ha reutilizado el algoritmo del post anterior cambiando el método minimize() por el descrito en este post.
La función que vamos a utilizar gradient_descent_with_momentum() admite, entre otros parametros:
num_mini_batch: Numero de lotes a dividir de la muestra suministada: 1 serie Gradiente Descendente hasta el tamaño completo de la muestra que ese caso estaríamos aplicando Gradiente Descendente Estocástico. Entre ambos límites, lo llamariamos Mini-Batchmomentum: Si queremos aplicar el momento a nuestro algoritmo, el parámetro se encontraría entre 0 y 1learning_rate_inicial: Tasa de aprendizaje
Todo el material se encuentra alojado en mi GitHub.
Resultados
| Modelo | Tiempo (Segundos) | Numero de Iteraciones | Numero De Muestras Consumidas | ECM |
|---|---|---|---|---|
| Gradient Descent | 5.29 | 370 | 37000000 | 0.12 |
| Mini-Batch Gradient Descent | 0.38 | 402 | 4020 | 0.089 |
| Mini-Batch Gradient Descent With Moment | 0.14 | 71 | 710 | 0.037 |
| Stocastict gradient descent With Moment | 0.41 | 478 | 478 | 0.026 |
Modelos Utilizados
Al ser una muestra homogenea y sin ruido, cabría esperar que con un pequeño numero de muestras de entrada al algortimo fuese suficiente. En los algoritmos que hemos aplicado el Momento (recordar que actúa como un filtro paso bajo desechando pequeñas alteraciones) solamente hemos necesitado menos del 1% de la muestra
Se puede apreciar que combinando la ejecución por Mini-Batch y aplicando Momento conseguimos una mejora significativa, sobretodo en el tiempo de calculo.
Analizando las gráficas se puede observar que para la primera solución, la trayectoria para alcanzar el mínimo local es siempre el de «mayor inclinación» (siempre va decayendo hasta alcanzar un mínimo local) mientras que si añadimos mini lotes hay pequeñas fluctuaciones (Solución 2) puesto que cada muestra puede tener distinta orientación.
En el caso de aplicar el Momento a los mini lotes se observa que se «asciende el ECM», unicamente es debido a la segunda ventaja que se describe en la introducción.
En el caso de la ultima solución hemos tenido que disminuir la tasa de aprendizaje para limitar el alcance de cada iteración y conseguir que el algoritmo convergiera.
Resultados
Aunque sabemos que los resultados son aproximados, lo que ya nos adelantaba la teoría se cumple en la practica: el estimador GradientDescentMomentum con Mini-Batch=10000 consigue el menor tiempo de computo. La razón que sea mas rápido que su homologo Mini-Batch=1 posiblemente sea la paralización vectorial del procesador
Segunda parte
Pero alguno me puede decir que estos resultados son muy aproximados, no se ha recurrido a encontrar los mejores hiperparámetros y todo se ha se ha entrenado, validado y testeado en la misma muestra. Cierto, pero esta primera parte estaba orientado a como construir cualquier modelo que nos imaginemos a partir de los gradientes calculados por TensorFlow.
En el siguiente post, ya teniendo definido nuestro modelo vamos a encontrar los hiperparametros que mejor se ajustan a la muestra por medio de GridSearchCV. Esto supone que la función creada para este post se tiene que transformar en un estimador con las reglas de sklearn